लॉगरिथम

लॉगरिथम : सोयीनुसार निवडलेली व एकापेक्षा मोठी असलेली धन संख्या आधारांक म्हणून घेऊन तिच्या घाताच्या रूपात कोणतीही संख्या मांडल्यास तिच्यातील घातांकाला त्या संख्येचा त्या आधारांकाचा लॉगरिथम म्हणतात. उदा., अ हा आधारांक घेतल्यास व क्ष ही सख्या क्ष = अपअशी मांडल्यास प हा क्ष चा अ आधारांकाचा लॉगरिथम होय आणि तो लॉगअ क्ष = प असा दर्शवितात. येथेअ,क्ष प या सत् संख्या संख्या आहेत, असे मानले आहे. या व्याख्येवरून क्ष या संख्येचे मूल्य धन असले पाहिजे, हे स्पष्ट आहे. गुणाकार, भागाकार, घात इ.गणितकृत्ये करण्यासाठी लॉगरिथमाचा फार उपयोग होतो, तसेच काही नैसर्गिक आविष्कारांच्या संदर्भातील समीकरणे व सूत्रे मांडण्यासाठी त्याचा उपयोग होतो.

इतिहास

लॉगरिथमांचा शोध  जॉन नेपिअर या स्कॉटिझ गणितज्ञांनी इ. स. १६१४ मध्ये लावला. त्याच सुमारास स्विस गणितज्ञ योस्त ब्यूर्गी यांनीही लॉगरिथमाविषयी लेखन केले होते. या दोघांना लॉगरिथमाच्या शोधाचे श्रेय देण्यात येते. त्यानंतर हेन्‍री ब्रिग्झ, आद्रिआन व्ह्‍लाक, जॉन वॉलिस व इतर अनेक गणितज्ञांनी लॉगरिथम विषयीच्या ज्ञानामध्ये भर घातली. लॉगरिथमांचे दोन प्रकार आहेत: (१) सामान्य लॉगरिथ व (२) स्वाभाविक लॉगरिथम. ब्रिग्झ यांनी १० हा आधारांक घेतल्याने गणनक्रिया कशी सोपी होते. हे दाखविल्यावर १० आधारांकाचे लॉगरिथम सामान्य लॉगरिथम’ म्हणून ओळखले जाऊ लागले. स्वाभाविक लॉगरिथमांना ‘नेपिअर लॉगरिथम’ असेही म्हणतात. या लॉगरिथमाकरिता e ही अपरिमेय संख्या आधारांक म्हणून वापरण्यात येते ४ दशांश स्थळांपर्यंतचे मूल्य २.७१८२ असे आहे. इ. नेपिअर यांनी ट्यूको ब्राए या जोतिर्विदांना आपल्या शोधाची कल्पना १५९४ मध्ये दिली आणि ती १६९४ मध्ये Mirifici logarithmorum canoni descriptio या ग्रंथाद्वारे प्रसिद्ध केली. १६२४ मध्ये ब्रिग्झ यांची कोष्टके प्रसिद्ध झाली. त्याच वेळी केल्पर यांची कोष्टकेही प्रसिद्ध झाली. गणितीय कोष्टके. १६३० पर्यंत लॉगरिथमाचा प्रकार झाला होता व ज्योतिविंद त्याचा वापर करू लागले होते. नेपिअर यांनी लॉगरिथामाचा आधारांक e हा प्रत्यक्ष वापरलेला नव्हता, तरी e आधारांकाच्या लॉगरिथमांना नेपिअर लॉगरिथम म्हणण्याचा प्रघात आहे. लॉगरिथमांचा शोध लावल्याबद्दल त्यांच्या गौरवार्थ हा प्रघात पडलेला आहे. ज्या वेळी लॉगरिथमाचा आधारांक निर्देशित केलेला नसेल त्या वेळी e आहे असे गृहीत धरले जाते. लॉगरिथमाचा उपयोग जवळजवळ तीनशे वर्षें सर्रास करण्यात येत होता. एकोणिसाव्या शतकातील गणकयंत्राच्या शोधानंतर व विसाव्या शतकातील इलेक्ट्रॉनीय संगणकाच्या शोधानंतर लॉगरिथमाचा उपयोग मोठ मोठ्या गणनक्रियांमध्ये मागे पडला, तरीही  गणकपट्टीच्या रचनेकरिता लॉगरिथमाचा आधार घेण्यात येतो.

मूलभूत नियम

लॉगरिथमाची व्याख्या घाताकाच्या संकल्पनेवर आधारलेली आहे. जर क्ष, अ > १ व प या सत् संख्या असतील आणि क्ष = अपअसेल, तर प = लॉगअक्ष या व्याख्येवरून, अ0 = १ असल्याने लॉगअ= ० व अ१ = अ असल्याने लॉगअअ = १हे नियम मिळतात. व्याख्येवरून हेही स्पष्ट होते की, एकापेक्षा मोठ्या असलेल्या सर्व धन संख्यांचे लॉगरिथम धन असतात आणि एकापेक्षा लहान असलेल्या सर्व धन संख्यांचे लॉगरिथम ऋण असतात.

अ, क, प, फ या सत् संख्या असतील, तर त्यांच्या संबंधीचे घातांकाचे नियम बीजगणित खालीलप्रमाणे आहेत :

(१) अप × अफ = अ प + फ

(२) अप ÷ अफ = अ प – फ

(३) (अप)फ = अ प फ

(४) (अ क)प = अ प × कप

(५) (अ / क)प = अप / कप

या नियमांवरून अ, य, र, प या संख्यांसाठी लॉगरिथमासंबंधीचे नियम खालीलप्रमाणे मिळतात.

(१) लॉगअ (य र) = लॉगअ य + लॉगअ र;

(२) लॉगअ (य/र) = लॉग अ य – लॉगअ र;

(३) लॉगअ यप = प लॉगअ य;

(४) लॉगअ पÖय = लॉगअ य १/प = १/प लॉगअ य

सामान्य लॉगरिथम

सामान्य लॉगरिथमाकरिता आधारांक १० घेतात हे वर आलेच आहे. लॉग१० १ = ० आणि लॉग १० = १ हे वरील विवेचनावरून स्पष्ट होईल. यावरून १ व १० यांमधील कोणत्याही संख्येचा सामान्य लॉगरिथम ० व १ यांमध्ये असला पाहिजे, हे उघड आहे. त्याचप्रमाणे १०२ = १०० असल्यामुळे १० व १०० यांमधील संख्येचा लॉगरिथम १ व २ मध्ये असला पाहिजे, तसेच १०० व १,००० यांमधील संख्येचा लॉगरिथम २ व ३ मध्ये असला पाहिजे. याप्रमाणे कोणत्याही संख्येचा लॉगरिथमाचा विचार करता येईल. लॉगरिथमाचे दोन भाग असतात. उदा., १.८७५०६ हा ७५ या संख्येचा लॉगरिथम विचारात घेतला, तर त्यामध्ये १ हा पूर्णांक आहे व .८७५०६ अपूर्णांक आहे. यापैकी १ या पूर्णांक भागाला लॉग पूर्णांश म्हणतात आणि अपूर्णांक भागाला लॉग अपूर्णांश म्हणतात. लॉगरिथाच्या कोष्टकामध्ये लॉग अपूर्णांश फक्त दिलेले असतात. लॉग पूर्णांश संख्येवरून काढता येते. त्याकरिता पुढील नियम वापरतात. दिलेल्या संख्येवरून पूर्णांक भागात जेवढे क असतील, त्यांपेक्षा लॉग पूर्णांश एकाने कमी असतो. उदा., २३,०१४.२५ या संख्येच्या लॉगरिथमामध्ये लॉग पूर्णांश ४ होईल. कोष्टकावरून लॉग अपूर्णांश भाग शोधताना दशांश चिन्ह विचारात घ्यावयाचे नसते. कारण दोन संख्यांमध्ये अंक तेच असून फरक फक्त दशांश चिन्हाचाच असेल, तर अशा संख्याच्या लॉगरिथमामध्ये फरक फक्त पूर्णांक भागाताच असतो. उदा., २,५३४ = २.५३४ × १०३

लॉग २५३४ = लॉग २.५३४ + ३.

१०० = १; १०–१ = ०.१; १०–२ = ०.०१; १०–३ =०.००१ यावरून असे दिसून येईल की, अपूर्णांकाच्या लॉगरिथमामध्ये लॉग पूर्णांश ऋण असणार. त्यांच्याकरिता लॉग पूर्णांश ठरविण्यासाठी पुढील नियम वापरतात : दशांश चिन्हानंतर जितकी शून्ये असतील त्यापेक्षा लॉग पूर्णांश १ ने जास्त असतो. उदा., ०.०००१०७ या संख्येत दशांश चिन्हानंतर तीन शून्ये आहेत म्हणून लॉग पूर्णांश -४ होईल व तो `४ असे लिहिण्याचा प्रघात आहे. लॉग अपूर्णांश मात्र नेहमी धनच असतो म्हणून एखाद्या संख्येचा लॉगरिथम`२.१३४५ असेल, तर त्याचा अर्थ -२ +.१३४५ असा घ्यायवाचा असतो.

प्रतिलॉगरिथम

लॉगरिथम दिलेला असल्यास त्यावरून मूळ संख्या शोधून काढण्याच्या क्रियेला प्रतिलॉगरिथम काढणे असे म्हणतात. प्रतिलॉरिथमाच्या सारणीमध्ये लॉग अपूर्णांश दिलेला असतो. त्यावरून मूळ संख्येतील अंक मिळतात व लॉग पूर्णांशावरून दशांश चिन्हांचे स्थान निश्चित करता येते. उदा., `२.०२२९४ या लॉगरिथचा प्रतिलॉगरिथम ०.०१०७ असा येतो.

उदाहरण

लॉगरिथमाचा उपयोग करून गुणाकार, भागाकार इ गणित कृत्ये कशी सुलभ होतात ते पुढील उदाहरणावरून स्पष्ट होईल.

(३१.६९)२ × ०.७९८

समजा  ------------------ याचे मूल्य म काढावयाचे आहे.

०.०८६३ × ३ √१०१.८६

आता

लॉग म = २ लॉग ३१.६९ + लॉग ०.७९८

-लॉग ०.०८६३ – १/३ लॉग १०१.८६

= २ × १.५००९ + १.९०२० – २.९३६०

-१/३ × २.००८०

= ३.२९८५.

३.२९८५ हा म चा लॉगरिथम आहे म्हणून त्याचा प्रतिलॉगरिथम म्हणजेच म चे मूल्य. ते १९८८.०० इतके येते. लॉगरिथमाच्या कोष्टकामध्ये दिलेली लॉगरिथमाची मूल्ये आसन्न (अंदाजी) मूल्ये असतात म्हणून लॉगरिथमाच्या साहाय्याने उदाहरण सोडविल्यावर येणारे उत्तर आसन्न मूल्य असते, हे लक्षात ठेवले पाहिजे.

स्वाभाविक लॉगरिथम

स्वाभाविक किंवा नेपिअर लॉगरिथमाकरिता आधारांक e ही अपरिमेय संख्या घेतात. e ही संख्या

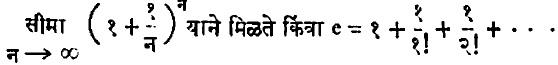सदर अनंत श्रेढीने मिळते. e चे मूल्य २.७१८२८....... असे आहे. e हा आधारांक योजण्याचे एक कारणम्हणजे त्यामुळे लॉगरिथाचे संगणन सुलभ होते व दुसरे कारण  कलनशास्त्रातील पुढील निष्कर्षात आढळून येईल : जर य = e क्ष, तरdय/dक्ष= य यावरून

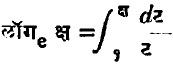अनुप्रसुक्त गणितशास्त्रामध्ये पुष्कळशा समस्यांची उत्तरे eक्ष या फलनावर आधारित असतात. उदा., अनम्य दोरीचा किंवा साखळीची समतोल स्थिती, विद्युत् मंडलातील क्षणिक प्रवाह, किरणोत्सर्गी (भेदक कण वा किरण बाहेर टाकणाऱ्या) द्रव्यांचे विघटन वगैरे.

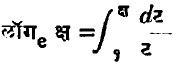या व्याख्येवरून लॉगरिथमाची संपूर्ण उपपत्ती व गुणधर्म काढता येतात व त्यावरून व्यस्त फलन→ फलन म्हणून eक्ष या फलनासंबंधीचे प्रमेय व अनंत श्रेढी ही प्रस्थापित करता येतात. टेलर

प्रमेयाचा → अवकलन व समाकलन उपयोग करून खालील श्रेढी मिळविता येते :

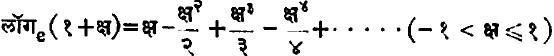या श्रेढीचा वापर करून लॉगरिथाचे संगणन करून पुरेसे आसन्न मूल्य काढता येते.

वरील श्रेढीपेक्षाही द्रूत अभिसारी श्रेढी खाली दिल्याप्रमामे मिळविता येते :

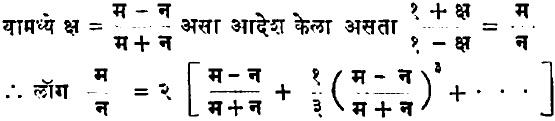
या श्रेढीतील थोडी पदे लॉगरिथमाचे मूल्य काढण्याकरिता पुरेशी येतात. उदा.,

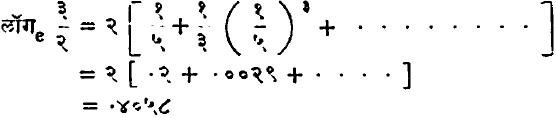
आधारांक बदलणे

स्वाभाविक लॉगरिथमापासून सामान्य लॉगरिथम कसे मिळवावे हे पुढे दर्शविले आहे. लॉगरिथमाचा आधारांक बदल्याण्याकरित पुढील सूत्राचा उपयोग होतो :

लॉगम क= लॉगख क × लॉगम ख,

यावरून लॉग१० क्ष =लॉगe क्ष × लॉग१० e

लॉग e याचे मूल्य ०.४३४२९ असे आहे. तेव्हा स्वाभाविक लॉगरिथमाला ०.४३४२२९ ने गुणिले असता सामान्य लॉगरिथम मिळतो. तसेच सामान्य लॉगरिथमाला २.३०३ ने गुणिले असता स्वाभाविक लॉगरिथम मिळतो.

सदसत् संख्यांचे लॉगरिथम

सामान्य किंवा स्वाभाविक लॉगरिथमामध्ये अ, क्ष, प या सर्व सत् आहेत असे गृहित धरले आहे व त्यांपैकी क्ष ही संख्या नुसती सत् नसून घनही आहे, असे मानले आहे. जर सत् संख्यांएवजी सदसत् संख्यांचा संख्या विचार केला, तर लॉगरिथमाची अनेक मूल्ये संभवतात. त्यांपैकी एका विशिष्ट मूल्याला प्रधान मूल्य म्हणतात. याचा खुलासा त्रिकोणमितीमधील पुढील दोन सिध्दांतावरून होईल :

(१) ‘ज्या’ व ‘कोज्या’ फलने आवर्ती असून त्यांचा आवर्तनांक २p आहे.

(२) eiq = कोज्या q + i ज्या q, (i = –1 व q अरीय मानात).

या दोन सिद्धांतांवरून असे दिसून येईल कि,

eiq= कोज्या q + i ज्या q

= कोज्या (२ म p+q) + i ज्या (२ म p + q)

= e (2 मp +q) i

समजा, क्ष = अप यामध्ये क्ष = प + i फ , प = त + i थ आणि अ = e आहे. आता,

प + i फ= eत + i थ

= eत (कोज्या थ + i ज्या थ)

= eत (कोज्या (२ म p + थ) + i ज्या (२ म p+ थ)

= eत + i (2 म p+थ)......... (१)

लॉगe(प + iफ) = त +i (२ म p + थ)

यात म कोणतीही पूर्णांक संख्या असल्यामुले लॉग e (प + iफ)ची मूल्ये अनंत मिळतील. या सूत्रात म = ० आणि –p < थ ≤pअसेल, तर त्या मूल्याला प्रधान मूल्य म्हणतात. सूत्र (१) मध्ये सत् आणि असत् भाग समान मांडून

प = eत कोज्या थ= eत कोज्या (२ म p+थ) आणि

फ = eत ज्या थ= eत ज्या (२ म p + थ)

ही समीकरणे मिळतील. यावरून प2 + फ२ = e2त हे सूत्र मिळते.

त = १/2 लॉगe(प२ + फ२) तसेच ज्या थ/कोज्या थ = फ/प

थ = स्प–१ फ/प म्हणजेच

लॉगe(प + iफ) = १/२ लॉगe (प2 + फ२) + i स्प–१ फ/प

हे प्रधान मूल्य होईल.

सदसत् संख्याच्या लॉगरिथमांवरून ऋण संख्यांचेही लॉगरिथम मिळविता येतील. उदा., वरील सूत्रात प = -१ आणि फ = ० असा आदेश करून

लॉगe (- १) = लॉगe(१) + i (p +२म p)

= i (p + २म p)

i चा लॉगरिथम काढावयाचा झाल्यास प = ० आणि फ = ० घेऊन

लॉगe(i) = i (p/२ + 2 म p).

तसेच प = e आणि फ = ० घेऊन

लॉगe e = १ + २म p i

म्हणजे e चा सत् लॉगरिथम १ असून सदसत् लॉगरिथम अनंत आहेत.

संदर्भ : 1. Austwick, K. Logarithms, New York, 1951.

2. Hartley, J. Logarithms , London, 1964.

3. Selby, P. H. Logarithms self-Taught , New York, 1964.

लेखक -  ल. वा. गुर्जर / स. ज. ओक

स्त्रोत - मराठी विश्वकोश